A research paper is a comprehensive document that presents the findings, analysis, and interpretations of a scholarly investigation into a particular topic or issue. It typically follows a structured format and is written for an academic or professional audience. Here are some key aspects of a research paper:

Title

The title of a research paper is a concise statement that captures the essence of the study. It should be clear, informative, and engaging, giving readers a glimpse of what to expect in the paper.

Abstract

The abstract is a summary of the entire research paper. It typically ranges from 150 to 300 words and includes the research problem, methodology, key findings, and conclusions. The abstract is often the first section of the paper and serves as a quick reference for readers to determine the relevance and significance of the study.

Introduction

The introduction sets the stage for the research paper by providing background information on the topic, defining key terms, and explaining the significance of the research. It also states the research question or hypothesis and outlines the structure of the paper.

Literature Review

The literature review critically evaluates existing research and scholarship related to the topic of the study. It identifies key concepts, theories, and methodologies used in previous studies, highlights gaps or inconsistencies in the literature, and provides a theoretical framework for the current research. The literature review helps situate the study within the broader academic discourse and demonstrates the novelty or contribution of the research.

Methodology

The methodology section describes the research design, data collection methods, and analytical techniques to address the research question. It includes details on participant recruitment, sampling procedures, data collection instruments, and ethical considerations. The methodology should be sufficiently detailed to allow other researchers to replicate the study and assess its validity.

Results

The results section presents the study’s findings clearly and organized. It may include descriptive statistics, tables, figures, or qualitative data excerpts to support the interpretation of results. The results section should focus on answering the research question or testing the hypothesis without interpretation or speculation.

Discussion

The discussion section interprets the results in light of the research question, compares them to previous studies, and explores their implications. It discusses the significance of the findings, addresses any limitations or biases in the study, and suggests avenues for future research. The discussion may also consider alternative or unexpected findings and offer possible explanations or theoretical frameworks to contextualize the results.

Conclusion

The conclusion summarizes the study’s main findings, restates the research question or hypothesis, and discusses their implications for theory, practice, or policy. It emphasizes the significance of the research and its contribution to the field while also acknowledging any limitations or areas for further investigation.

References

The references section lists all sources cited in the research paper. It follows a specific citation style (e.g., APA, MLA, Chicago) and includes complete bibliographic information for each source, such as author(s), title, publication year, and source location (e.g., journal article, book, website). The references allow readers to verify the accuracy of the information presented in the paper and locate additional resources for further reading.

Research papers are a fundamental part of academic and scientific discourse, advancing knowledge within a particular field or discipline. They undergo peer review by experts in the field to ensure rigor, validity, and relevance before publication in scholarly journals or presentations at conferences.

Needs help with similar assignment?

We are available 24x7 to deliver the best services and assignment ready within 3-4 hours? Order a custom-written, plagiarism-free paper

Get Answer Over WhatsApp Order Paper Now

The literature review section of a research paper critically evaluates and synthesizes existing scholarly literature relevant to the research topic. It serves several important purposes in the research process:

Establishing Context

The literature review begins by providing background information on the research topic situating it within the broader academic discourse. This involves identifying key concepts, theories, and debates related to the topic and tracing the evolution of research in the field.

Identifying Gaps and Controversies

It identifies gaps, inconsistencies, or controversies in the existing literature, highlighting areas where further research is needed. This may involve discussing conflicting findings, methodological limitations, or overlooked topics within the field.

Theoretical Framework

The literature review provides a theoretical framework or conceptual model for the study, drawing on relevant theories or conceptual frameworks to guide the research design and interpretation of findings.

Methodological Approaches

It examines the methodological approaches used in previous studies, evaluating their strengths and weaknesses and informing the choice of research methods for the current study. This may involve discussing different research designs, sampling techniques, data collection methods, and analytical approaches employed in the literature.

Synthesizing Findings

The literature review synthesizes key findings from previous research, summarizing empirical evidence and theoretical insights relevant to the research question. This synthesis helps build a cumulative body of knowledge and provides a basis for interpreting the current study’s findings.

Identifying Research Gaps

Based on the review of existing literature, the literature review identifies specific research gaps or unanswered questions that the current study aims to address. This helps justify the need for the study and delineates its contribution to the field.

Framework for Analysis

Finally, the literature review may inform the analytical framework or research approach used in the study, guiding how to analyze and interpret the data collected. This ensures that the research builds on existing knowledge and meaningfully extends theoretical or empirical insights.

Example

Title: “Navigating the Landscape: A Critical Review of Existing Research on Social Media Use and Adolescent Well-being”

Literature Review:

The impact of social media use on adolescent well-being has been a topic of growing interest and concern among researchers and practitioners alike. Previous studies have explored various dimensions of this relationship, including its effects on mental health, self-esteem, social relationships, and academic performance. While some studies have found associations between excessive social media use and negative outcomes such as depression, anxiety, and cyberbullying, others have reported mixed or null findings. Methodological differences may contribute to these discrepancies, such as measurement instruments, sample characteristics, and study designs. Research on potential protective factors, such as social support, parental monitoring, and digital literacy, remains relatively sparse. This literature review synthesizes findings from quantitative and qualitative studies, highlighting methodological considerations and theoretical frameworks employed in previous research. It identifies gaps in the literature, such as the need for longitudinal studies, cross-cultural comparisons, and nuanced examinations of specific social media platforms and usage patterns. Building on this foundation, the current study aims to contribute to understanding the complex relationship between social media use and adolescent well-being, considering individual and contextual factors that may shape this dynamic interplay.

Note: in a research paper, the review should include citations of the previous work or just be specific to the source of information, as shown below

Literature Review with Citations:

The impact of social media use on adolescent well-being has been a topic of growing interest and concern among researchers and practitioners alike. Previous studies have explored various dimensions of this relationship, including its effects on mental health, self-esteem, social relationships, and academic performance (Jones et al., 2018; Smith & Brown, 2019). While some studies have found associations between excessive social media use and negative outcomes such as depression, anxiety, and cyberbullying (Gupta et al., 2017; Lee & Lee, 2020), others have reported mixed or null findings (Choi & Park, 2016; Wang et al., 2018). Methodological differences, such as measurement instruments, sample characteristics, and study designs, may contribute to these discrepancies (Ryan & Xenos, 2011). Research on potential protective factors, such as social support, parental monitoring, and digital literacy, remains relatively sparse (Huang & Liu, 2019; Orben & Przybylski, 2019). This literature review synthesizes findings from quantitative and qualitative studies, highlighting methodological considerations and theoretical frameworks employed in previous research. It identifies gaps in the literature, such as the need for longitudinal studies, cross-cultural comparisons, and nuanced examinations of specific social media platforms and usage patterns (Livingstone & Smith, 2014; Twenge & Campbell, 2018). Building on this foundation, the current study aims to contribute to understanding the complex relationship between social media use and adolescent well-being, considering individual and contextual factors that may shape this dynamic interplay.

Needs help with similar assignment?

We are available 24x7 to deliver the best services and assignment ready within 3-4 hours? Order a custom-written, plagiarism-free paper

Get Answer Over WhatsApp Order Paper Now

Quantitative analysis is a cornerstone of modern decision-making, offering a systematic approach to understanding data, identifying patterns, and predicting future trends. From finance and economics to healthcare and engineering, this method leverages numerical data to derive meaningful insights that inform strategies, improve outcomes, and drive innovation.

What is Quantitative Analysis?

Quantitative analysis involves using mathematical and statistical techniques to analyze numerical data. It contrasts with qualitative analysis, focusing on non-numerical data such as text, images, and observations. Quantitative analysis seeks to uncover relationships, test hypotheses, and make data-driven decisions by employing tools such as statistical tests, models, and computational algorithms.

Core Principles of Quantitative Analysis

Data Collection

Effective quantitative analysis begins with robust data collection. The data can be gathered from various sources, including surveys, experiments, sensors, and existing databases. Ensuring accurate, relevant, and comprehensive data is critical for reliable analysis.

Descriptive Statistics

Descriptive statistics summarize and describe the main features of a dataset. Key measures include:

Mean: The average value.

Median: The middle value when data is ordered.

Mode: The most frequently occurring value.

Standard Deviation: A measure of data dispersion around the mean.

These statistics provide a snapshot of the data’s overall distribution and variability.

Inferential Statistics

Inferential statistics allow analysts to make predictions or inferences about a population based on a sample of data. Techniques include:

Hypothesis Testing: Evaluating assumptions about a dataset (e.g., t-tests, chi-square tests).

Confidence Intervals: Estimating the range within which a population parameter lies with a certain confidence level.

Regression Analysis: Modeling relationships between variables (e.g., linear regression, logistic regression).

Data Visualization

Visualizing data through charts, graphs, and plots helps to identify trends, patterns, and anomalies. Common visualization tools include:

Histograms: Show frequency distributions.

Scatter Plots: Display relationships between two variables.

Box Plots: Highlight data spread and outliers.

Modeling and Simulation

Quantitative analysis often involves creating models to simulate real-world processes. These models can range from simple linear equations to complex algorithms like machine learning models. Simulations can test various scenarios and predict outcomes, aiding in decision-making under uncertainty.

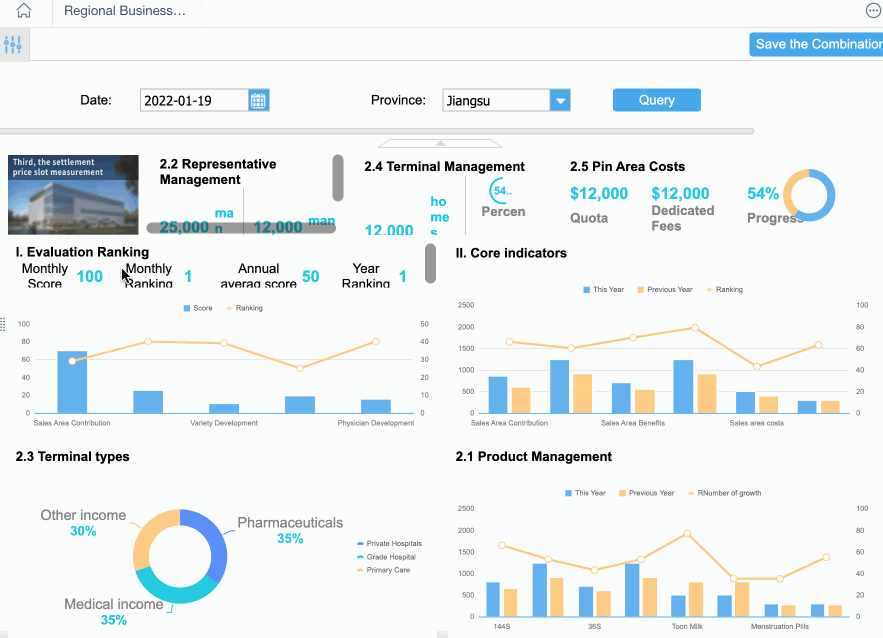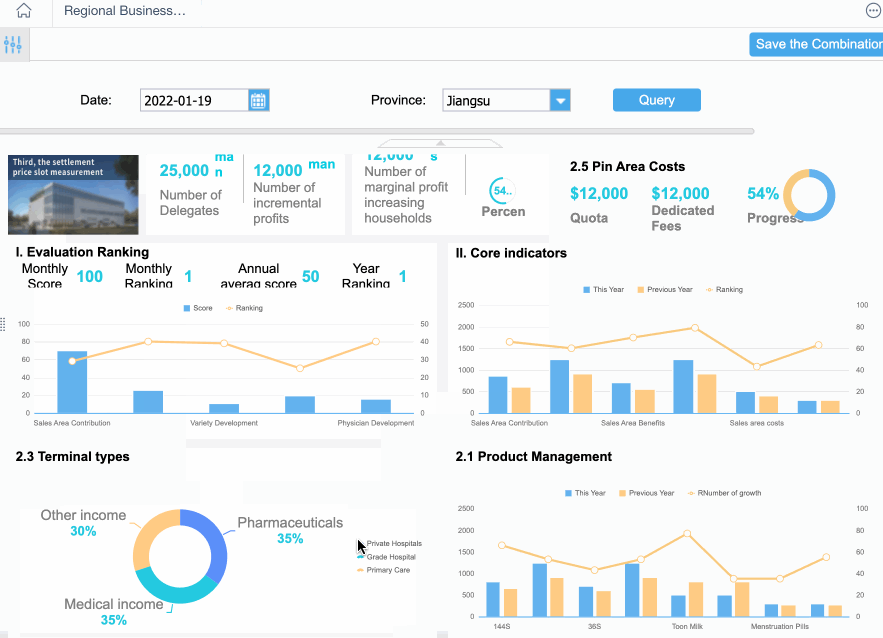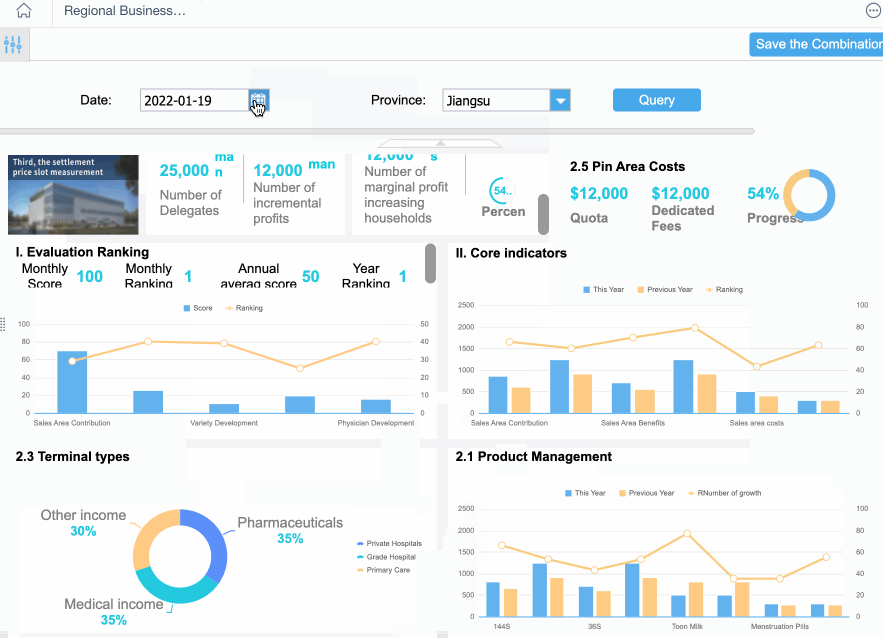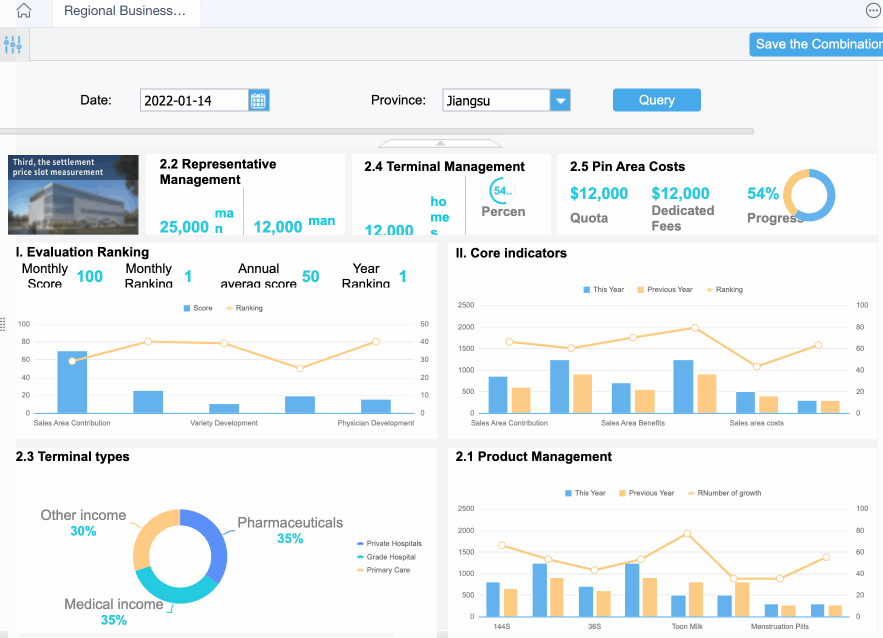
Applications of Quantitative Analysis

Finance and Economics

Quantitative analysis is essential for portfolio management, risk assessment, and pricing strategies in finance. Economists use quantitative methods to analyze economic indicators, forecast economic trends, and evaluate policy impacts.

Healthcare

Quantitative analysis in healthcare helps in clinical trials, epidemiological studies, and healthcare management. Researchers can identify risk factors, track disease outbreaks, and optimize treatment protocols by analyzing patient data.

Engineering and Manufacturing

Engineers use quantitative methods for quality control, reliability testing, and process optimization. Manufacturing processes benefit from data-driven improvements in efficiency, reducing costs, and enhancing product quality.

Marketing

Marketers employ quantitative analysis to segment markets, measure campaign effectiveness, and understand consumer behavior. Data-driven insights enable targeted marketing strategies and improve return on investment (ROI).

Challenges in Quantitative Analysis

Data Quality

The accuracy and reliability of conclusions depend on the quality of the data. Poor data quality can lead to misleading results and flawed decisions.

Complexity

Advanced quantitative methods can be complex and require specialized knowledge. Proper training and expertise are necessary to apply these techniques effectively.

Interpretation

Interpreting quantitative results correctly is crucial. Analysts must avoid common pitfalls such as overfitting models, misinterpreting correlations, and ignoring confounding variables.

Conclusion

Quantitative analysis is a powerful tool that transforms raw data into actionable insights. By employing rigorous methods and leveraging advanced technologies, it helps organizations and researchers make informed decisions, solve complex problems, and uncover new opportunities. As the world becomes increasingly data-driven, the importance of quantitative analysis will only continue to grow, driving progress across various fields and industries.

Embracing quantitative analysis enhances our understanding of the world and equips us with the tools to shape a better future through informed and strategic decision-making.

 

Needs help with similar assignment?

We are available 24x7 to deliver the best services and assignment ready within 3-4 hours? Order a custom-written, plagiarism-free paper

Get Answer Over WhatsApp Order Paper Now